P2P文件共享系统中网络编码译码算法
摘要
P2P 文件共享在互联网上越来越受欢迎,其中基于 P2P 技术的内容分发系统 BitTorrent 是最广泛应用的一种。然而,该系统存在一些限制,包括对种子节点的依赖性过强、文件块选择算法不够优化以及网络带宽利用率较低等问题。因此,本论文着重研究了 P2P 文件共享系统中网络编码译码算法的设计与优化,并探讨了这些算法在改进型 BitTorrent 内容分发系统设计中的应用。
本文首先介绍了有限域运算的基础知识和基本概念,以及有限域构造的方法。同时,深入分析了网络编码理论的提出及其在网络传输中的优势,并对 BitTorrent 系统和协议进行了详细探讨。通过对有限域构造方式的分析,设计并实现了 GF(256)的有限域运算算法。分析并实现了分代的随机线性稀疏网络编码算法,并通过实验确定了最佳的稀疏度为 0.95,从而在不增加数据包数量的情况下提升了 1 倍解码速率。为减少内存使用,选择了 128MB 的分代大小和 1MB 的分块大小。同时,对高斯约旦消元算法进行了优化,增加了线性相关性检测功能,以减轻线性相关数据包对解码速率的影响,并通过并行化设计将解码速率提高了 4 到 5 倍。最后,本文设计并实现了基于网络编码的编译码算法的分布式文件共享系统 PeerCodeX。
第一章 绪论
1.1 研究背景与意义
随着计算机和网络技术的不断进步,越来越多的数据和信息需要在全球范围内传输和分发。这些数据和信息包括游戏更新、软件安装包、影视资源、在线直播等。为了确保这些数据和信息能够快速、高效地传输和分发到用户所在的地区,需要采用适当的内容分发技术。
通常传统的文件传输方式是通过中心服务器来实现的,服务器负责管理所有客户端的网络连接并向它们分发内容。然而,这种方式存在一些限制。例如,传输速度受到服务器带宽的限制,因为传输大型文件需要更多的带宽以缩短传输时间,所以受限于服务器带宽,可以提供服务的客户端数量会受到限制。此外,传统的文件传输方式也会给服务器带来较大的负载,例如服务客户端数量过多时,因为网络带宽不足,每个客户端所分配的带宽十分有限,所以每个客户端需要较长的服务时间,服务器需要同时维护大量的网络连接。同时,在面对“Flash Crowd”时,因为服务器资源不足,无法在短时间内提供增量服务,因此服务器可能会出现拒绝服务的情况。
为了解决以上问题,出现了 CDN(内容分发网络[1])和 P2P(点对点)两种内容分发的技术路径。
CDN 是一种分布在全球各地的服务器网络,可用来加速内容的传输。CDN 的工作原理是,通过将网站的静态内容(如图片、脚本、样式表等)缓存在全球分布的服务器上,当用户访问一个网站时,CDN 会从距离用户最近的服务器上获取所需内容提供给用户。这可以大大降低响应时间并提高传输速率,因为用户不必等待内容从远程服务器传输到他们所在的地区。除此之外,CDN 技术还可以通过负载均衡和容错机制,确保网站在大量访问时不会因为服务器过载而崩溃,提高了网站的可用性和稳定性。同时,CDN 技术还可以降低源站服务器的请求量和压力,从而降低了服务器成本。不过,CDN 技术也有一些缺点。首先,使用 CDN 技术需要购买 CDN 服务,并且需要对网站进行一定的调整和配置,从而增加了网站部署的成本。其次,CDN 服务器上的缓存可能不会及时更新,导致用户访问的不是最新的数据,从而影响网站的实时性和准确性。最后,CDN 技术是基于分布式架构实现的,但是如果某个 CDN 节点出现故障,可能会影响全局的服务质量。其中主要案例是全球最大的 CDN 提供商 Cloudflare 在 2022 年 6 月 21 日因为分发了错误的配置文件,导致全球 19 个数据中心下线,尽管这些数据中心仅占 Cloudflare 的 CDN 网络的一小部分(4%),但总请求数的 50% 受到了影响,这直接导致了全球大量网络服务中断 3 小时[2]。
基于 P2P 技术的内容分发系统最著名的就是 BitTorrent[3]。BitTorrent 允许用户之间直接分享文件,而是通过中心服务器下发的方式。在使用 BitTorrent 协议的过程中,每个用户都是文件的源,同时也是文件的端。这使得文件的传输速度更快,因为用户之间直接传输文件而不是通过中心服务器。然而,它存在对种子节点的依赖性太强的问题。如果种子节点出现故障或者停止服务,就会导致客户端无法发现网络中其他的客户端,伴随着旧节点的退出和新节点无法加入,该网络就会逐渐消亡。其次,BitTorrent 协议的文件块选择算法只能达到局部最优[4],因此在某些情况下可能会导致文件传输效率低下。虽然目前又发展出 DHT 网络技术,可以在无 Tracker 的情况下下载,但其同样需要维护分布式哈希表,而且也提高了网络的复杂性。
在通信网络中,通常使用独立的数据流和共享的网络资源来传输信息。但是,网络编码[5]是信息论的一个新领域,它打破了这种假设。使用网络编码技术,节点可以将多个输入数据包重新组合成一个或多个输出数据包,而不是简单地转发数据。通过这种方式,最终节点只需要获得足够数量的已编码数据包,就能解码出原始文件,而不需要特定内容的数据包。这意味着,网络编码技术可以被用来压缩网络流量,从而进一步提高网络吞吐量。在 P2P 文件传输系统中,使用网络编码算法不仅具有分布式点对点文件传输系统的优点,而且可以解决基于传统的转发策略的缺点。
网络编码算法可以有效地解决分布式系统中数据包传播调度的问题,使节点能够根据本地信息决定如何传播数据包,从而缓解块传播问题并更好地利用可用的网络容量。此外,网络编码系统非常稳健,可以应对服务器和节点突然离开的情况[6]。使用网络编码后,节点可以在服务器仅将文件的一个副本上传到系统后不久就离开,或者在完成下载后立即离开,而仍能够完成下载。相比之下,如果没有网络编码,如果服务器和一些对等点突然离开,原始文件或源编码文件的某些块会消失,其他节点将无法完成下载。因此,即使在极端情况下,使用网络编码的节点也能够完成下载,并且在处理网络流量突增(即“Flash Crowd”)时也能提高网络效率。
因为网络编码算法不再使用传统的转发策略,而是需要对文件内容进行整体编码,这使得每个节点发出一个编码后的数据包都需要读取文件的全部内容并对其进行编码操作,此步骤会大幅增加对内存和计算资源的开销,同时因为需要读取文件的完整内容,这会对硬盘产生大量读操作,其不仅会降低网络编码的速度,同时还会降低硬盘寿命。因此对网络编码的编译码算法研究与优化不仅可以更好地利用网络编码在 P2P 领域的算法优势,还能降低网络编码过多的内存和计算资源占用以及解决硬盘瓶颈问题。
1.2 网络编码的国内外研究现状
在传统的路由机制中,中间节点(如路由器和交换机)只会对数据包进行存储和转发,无法叠加信息。因此,在多播传输环境中,通常无法达到最大流最小割定理中所确定的最大传输容量。然而,在 2000 年,香港中文大学的 Rudolf Ahlswede 在《IEEE Transactions on Information Theory》杂志上提出了网络编码[5]的概念,并从理论上证明了如果中间节点能够以合适的方式对传输的信息进行编码,则该系统就能实现理论上的最大传输率。随后,香港中文大学的李硕彦教授、杨伟豪教授和蔡宁教授提出了线性网络编码,指出线性网络编码能够在多播环境中达到网络容量[7]。为了解决分布式网络环境中的编码问题,Tracey Ho 提出了随机网络编码,即随机选择系数进行编码[8]。Koetter Ralf 等人则提出了网络编码的代数框架,即可以使用代数理论来解决网络编码的系数问题[9]。这些研究成果进一步完善和丰富了网络编码理论。网络编码通过将数据包进行编码并重新组合,彻底颠覆了传统通信网络对信息的处理方式,实现了信息论中的最大传输率。因此,网络编码在信息论领域具有划时代的意义。
网络编码作为一种信息处理算法,在网络通信的各个协议层、文件存储、信息安全等领域都有突破性的贡献,因为研究目的为 P2P 文件共享系统中网络编码译码算法,所以这里只介绍网络编码在 P2P 领域的研究进展。
2006 年,麻省理工学院的学者提出了一种分散算法,用于计算最小成本子图,以便在编码网络中建立多播连接。这些算法与现有的构建网络编码的分散方案相结合,形成了一种完全分散的方法,可实现最低成本的组播。与主流方法基于有向斯泰纳树问题的近似算法形成鲜明对比,后者通常假定计算具有完全的网络知识,并且是次优的。此外,他们还考虑了在有定向点对点链接的网络中固定速率组播的基本问题之外的扩展,并研究了弹性速率需求的情况以及在无线网络中实现最小能量组播的问题[10]。佐治亚理工学院的 Christos Gkantsidis 和微软研究院的 Pablo Rodriguez 提出一个基于网络编码的大文件内容分发的新方案[6]。通过网络编码,分发网络的每个节点都可以生成和传输编码的信息块。编码过程引入随机化简化了块的传播调度,从而使分发更高效。2017 年匈牙利布达佩斯科技经济大学的 Patrik J. Braun、Péter Ekler 和德国德累斯顿工业大学的 Frank H. P. Fitzek 提出了一个使用 WebRTC 建立浏览器与浏览器直接连接的应用[11]。为基于浏览器的 P2P 流设计了两个协议 WebPeer 和 CodedWebPeer。WebPeer 是一个传统的 P2P 协议,而 CodedWebPeer 是一个网络编码增强的 P2P 协议。通过他们的系统,证明了使用 WebRTC 的 P2P 辅助 VOD 流是可以完成的。并且它的吞吐量比传统的客户端-服务器设置高出 70%。此外,通过应用网络编码,网络的性能进一步提高。
2009 年,华中科技大学提出了一种 P2P 流媒体点播系统的网络编码解决方案[12]。该方案采用了随机线性网络编码技术。通过网络编码,可以提高带宽的利用率和缓存空间的上传能力,该方案降低了对等节点的平均下载时间。2011 年,华中科技大学的杨军等人提出了一种基于网络编码回馈的拓扑感知机制(TANCF),以帮助进行网络拓扑感知[13]。该机制利用层次化网络中节点的回馈,探测信源到节点的可达路径信息。通过可达路径信息和关联矩阵之间的紧密关系,可以构建关联矩阵并优化网络编码系统的参数。2012 年,西安电子科技大学提出一种基于信任的网络编码算法,即 CNST 算法,它可以找到网络中的高信任度节点。该算法不仅可以实现网络组播的理论容量,而且在网络规模较大时,可以减少网络编码操作的执行时间,提高网络的健壮性[14]。2013 年清华大学的崔来中综述了现有互联网点到多点传送机制的解决方案和现有 P2P 流媒体传送的热点问题,提出了一个 P2P 流媒体传送性能优化研究框架,包括:传送拓扑、传送调度和流量优化三个部分,并针对不同部分提出了不同的解决方案[15]。之后,国内陆续在基于网络编码的 P2P 文件传输上做了相应研究。
当前,文件分发在软件安装包、游戏更新文件、网络流媒体和短视频等领域中非常常见。由于这些领域对文件分发的要求日益提高,同时 CDN(内容分发网络)的成本不断增加,这使得分布式点对点文件传输重新受到关注。网络编码可以解决 BitTorrent 协议的不足之处,因此,当前的发展趋势是在 P2P 领域优化网络编码的应用,以提高网络利用率并提高文件传输效率。
1.3 主要工作与组织结构
本文主要研究基于随机网络编码的编译码算法,在随机线性网络编码的基础上进行相关改进,从而提高编译码效率。同时对 BitTorrent 系统的优缺点进行分析,并修改 BitTorrent 的种子文件表示以及协议内容,同时对 BitTorrent 系统结构进行改造以适应网络编码技术的应用,最后对算法效率和改进后的 P2P 系统进行性能分析。
本论文共有五章,内容安排如下:
第一章:绪论,阐明了 P2P 领域中网络编码算法的研究背景以及意义,回顾了 P2P 技术以及网络编码的研究现状,并介绍本文主要工作。
第二章:首先概述网络编码的相关知识,之后介绍网络编码的编译码过程;同时介绍有限域的相关知识;最后对 P2P 技术的典型代表 BitTorrent 协议及其工作原理进行分析,并指出其存在的缺点。
第三章:首先介绍有限域运算的算法实现,其次介绍了网络编码编译码算法的改进设计,最后介绍了基于网络编码的 P2P 系统设计。
第四章:将对第三章讲述的编译码算法进行性能分析,比较改进算法相较于基础算法带来的性能提升,同时分析改进后的 P2P 系统的优劣。
第五章:归纳全文的研究和实验工作,对论文中存在的缺陷进行分析,并展望未来的工作和研究重点。
第二章 网络编码及 BitTorrent 系统的基础知识
本章将对网络编码与 BitTorrent 系统相关的基础知识进行介绍,首先介绍有限域的理论知识,之后介绍网络编码的基本概念,最后给出 BitTorrent 系统的深入分析。
2.1 有限域运算
有限域[16](Finite Field),也被称为伽罗瓦域(Galois Field),是一种数学结构,是在有限集合上定义了加法和乘法运算的数学对象。它是许多领域的核心,例如密码学、编码理论、代数几何等。
2.1.1 有限域的概念
由于计算机只能表示有限个元素的集合,因此在密码学中会更多地考虑有限域的情况,可以证明有限域的阶必须是一个素数的幂 p^n(n 为正整数),因此有限域通常记作 GF(p^n)。
在有限域上定义了两个二元运算,加法和乘法,满足以下条件:
-
加法和乘法都是封闭的,即对于任意两个元素 $a$ 和 $b$,$a+b$ 和 $ab$ 也属于有限域。
-
加法是可交换的,即对于任意两个元素 $a$ 和 $b$,$a+b=b+a$。
-
加法是可结合的,即对于任意三个元素 $a$、$b$ 和 $c$,$(a+b)+c = a+(b+c)$。
-
存在加法的单位元素 $0$,满足对于任意元素 $a$,$a+0=a$。
-
对于任意元素 $a$,存在其加法逆元素 $-b$,满足 $a+(-b) = 0$。
-
乘法是可交换的,即对于任意两个元素 a 和 b,$ab=ba$。
-
乘法是可结合的,即对于任意三个元素 $a$、$b$ 和 $c$,$(ab)c = a(bc)$。
-
存在乘法的单位元素 $e$,满足对于任意元素 $a$,$a×e=a$。
-
对于任意非零元素 $a$,存在其乘法逆元素 $a-1$,满足$aa-1=1$。
2.1.2 有限域的构造方式
可以通过两种方式构造有限域,一种是基于素数的有限域,一种是基于多项式的有限域[17],在构造有限域的过程中,可以看到以上规则的应用。
基于素数的有限域构造以 $GF(p)$ 为例,$p$ 是一个质数,它的元素包括 $0, 1, 2, …, p-2, p-1$ 。加法和乘法运算都是在模 $p$ 的基础上进行的。在 $GF(p)$ 中,加法运算定义为:
$a+b \equiv c(mod (p))$ (2-1)
乘法运算定义为:
$ab \equiv d(mod (p))$ (2-2)
其中 $\equiv$ 表示模 $p$ 同余。
对于加法和乘法,$0$ 为加法的单位元素,即对于任意元素 $a$,$a+0=a$。$1$ 为乘法的单位元素,即对于任意元素 $a$,$a×1=a$。对于任意非零元素 $a$,它的加法逆元为 $-p mod(p)$!,即 $a+(-a) \equiv 0(mod(p))$;它的乘法逆元为 $a^{p-2}$,即$aa^{p-2} \equiv 1(mod(p))$。
有限域 $GF(q)$ 也可以通过多项式进行构造,其中 $q = p^{m}$,其中 $p$ 是一个质数,$m$ 是一个正整数。它的元素集合包括 $GF(p)$ 上的 $m$ 次多项式。同样在 $GF(q)$ 上定义了加法和乘法运算,满足有限域的九个条件。
具体地,对于一个 $m$ 次多项式 $f(x)$,其系数属于 $GF(p)$,即 $f(x)=a_{0}+a_{1}x+a_{2}x^{2}+ … + a_{m-1}x^{m-1}$,其中 $a_{i}$ 属于 $GF(p)$ 。在运算中,系数运算以 $p$ 为模数,即遵循有限域 $GF(p)$ 上的运算规则。若乘法运算的结果是次数大于 $m-1$ 的多项式,那么须将其除以某个次数为 $m$ 的既约多项式 $m(x)$ 并取余式。在 $GF(q)$ 中,加法和乘法的运算都是模一个 $m$ 次不可约多项式的结果。一个 $m$ 次多项式是不可约的,当且仅当它不能被分解为两个次数小于 $m$ 的多项式的乘积。
在 $GF(q)$ 中,加法运算可以表示为:
$f(x)+g(x) \equiv h(x)(mod(m(x)))$ (2-3)
乘法运算可以表示为:
$f(x)g(x) \equiv k(x)(mod(m(x)))$ (2-4)
其中,$h(x)$ 和 $k(x)$ 是模 $m(x)$ 意义下的多项式余数。在 $GF(q)$ 中,$0$ 和 $1$ 分别表示加法和乘法的单位元素,对于任意非零元素 $f(x)$,它的加法逆元为$-f(x) mod (m(x))$,乘法逆元为$f(x)^{-1} mod (m(x))$。
2.2 网络编码理论
2.2.1 引言
如今的网络通信都有相同的基础原理,网络中的数据都是以共享通信信道的方式传输,在网络中数据通过各种协议头来寻址及编码解码,即数据本身是独立的。网络编码在信息论中的打破了这个假设。网络中的节点可以将输入数据包重新组合为一个或多个输出数据包,相较于传统的转发策略,网络编码有更优秀的性质。
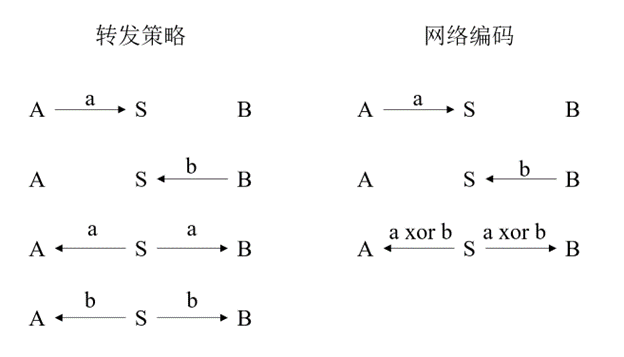
图 2.1 一个简单的网络编码示例
如图 2.1 所示,在无线环境中,如果节点 A 和节点 B 要互相交换数据包,在转发策略中,A 和 B 需要在两个时序中分别将数据传输给中间节点 S,之后 S 再通过两个时序分别广播数据包 a 和数据包 b。而在网络编码中,中间节点 S 收到数据包 a 和数据包 b 后,在一个时序中广播 a⊗b,节点 A 接收到这个数据包后,将其与自身所有的数据包 a 进行异或运算即可获得数据包 b,节点 B 可以以同样的方式获得数据包 a。该案例中通过网络编码即可减少一个时序的传输用时[18]。
下面先介绍最大流最小割定理[19],再以蝴蝶网络为例解释网络编码如何帮助提高网络的吞吐量。
2.2.2 最大流最小割定理
在一个流网络中,可以定义一个源点 $s$ 和一个汇点 $t$ ,以及一组有向边 $(u, v)$,其中 $u$ 和 $v$ 是网络中的节点,每条边 $(u, v)$都有一个容量 $c(u, v)$ ,表示该边最大可以承载的流量。还可以定义一个流函数 $f(u, v)$ ,表示从节点 $u$ 到节点 $v$ 流过的流量。
根据流网络的定义,需要满足以下三个条件:
- 容量限制条件:对于任意的 $(u, v)$,流函数 $f(u, v)$ 不超过容量 $c(u, v)$ ,即 $f(u, v) ≤ c(u, v)$。
- 流量守恒条件:对于任意的节点 $u$ ,流进节点 $u$ 的总流量等于流出节点 $u$ 的总流量,即 $\sum_{v}f(u,v) = \sum_{v}f(v,u)$。
- 非负性条件:对于任意的 $(u, v)$,流函数 $f(u, v)$ 是非负数,即 $f(u, v) ≥ 0$。
一个流的值是指从源点 $s$ 到汇点 $t$ 的总流量,即 $|f|=\sum_{v}f(s, v)-\sum_{v}f(v,s)$。
一个割是指将节点分成两个部分 $S$ 和 $T$,其中 $s \in S$ 且 $t \in T$,并且对于所有的 $(u, v)$,如果 $s \in S$ 且 $t \in T$,那么称该边横跨割,否则称该边不横跨割。一个割的容量是指所有横跨割的边的容量之和,即$C(S, T) = \sum_{u \in S, v \in T} c(u, v)。
现在可以给出 Max-Flow Min-Cut 定理的公式表述:
在一个流网络中,最大流的值等于最小割的容量,即 $|f| = C(S, T)$。
2.2.3 蝴蝶网络
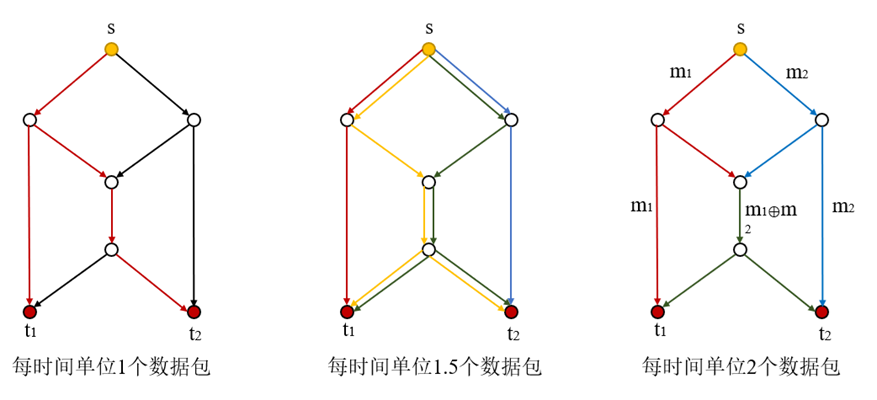
图 2.2 网络编码提高蝴蝶网络吞吐率的示例
图 2.2 以蝴蝶网络为例,其展示了网络编码对提高网络吞吐量的显著作用。在图 2.2(1)中,网络以最基础的转发策略方式传输数据,在一个时间单位内,只能利用 9 条网络线路中的 6 条,网络线路利用率为 67%,传输速率为每个单位时间 1 个数据包;在图 2.2(2)中,网络以分组传输的方式传输数据,在一个时间单位内可以利用全部线路,但有 4 条线路的利用率仅为 50%,因此,整体上网络线路利用率为 78%,传输速率为每个单位时间 1.5 个数据包;在图 2.2(3)中,使用了网络编码理论,中间的节点在同时接收到数据包 m_1 和 m_2 之后,对其进行异或运算,之后将数据传输到下一个节点,t_1 接收到的数据为 m_1 和 m_1⊗m_2,此时 t_1 可以解出数据 m_2,同理,t_2 可以获得数据包 m_1 和 m_2,此时线路利用率为 100%,传输速率为每个时间单位 2 个数据包。
2.3 BitTorrent 系统
BitTorrent 协议是一种用于大规模文件分发的协议,它利用了用户之间的协作,从而使得文件分发更加高效。BitTorrent 协议的基本原理是将要分发的文件分成若干个分块,每个分块的大小通常为 256KB 到 1MB 不等,然后通过 Tracker 服务器将文件的信息发布给所有的 Peer 节点。Peer 节点之间互相交换已经下载的分块,直到所有的分块都被下载完成。
2.3.1 Bencoding 编码
Bencoding[20]是一种简单的二进制数据编码格式。Bencoding 格式支持四种数据类型:String、Integer、List 和 Dictionary。其中 Integer 类型用“i”和“e”来标记开始和结束,String 类型用长度和冒号标记开始,List 和 Dictionary 类型则使用“l”和“d”来标记开始和结束。 BT 种子文件是一个 Bencoding 编码的字典,包含两个主要的键:announce 和 info。其中 announce 对应 BT Tracker 的 URL,info 包含资源信息的字典。该字典包含关键字,如资源名称(name)、每个分片的长度(piece length)和 SHA1 哈希值(piece)等。文件长度键(length)代表单文件长度,如果有多个文件则使用文件列表键(files),其中每个元素都是一个字典,代表一个文件,包含文件长度(length)和相对路径名(path)。其他可选键包括备用 BT Tracker 的 URL(announce-list)、种子的创建时间(creation date)、制作者的备注信息(comment)和生成种子文件的 BT 客户端软件信息(created by)。客户端向 BT Tracker 发送请求的返回数据同样以 Bencoding 格式编码。
2.3.2 BitTorrent 系统工作原理
BitTorrent 作为一个分布式文件共享系统,其工作需要各个客户端之间的协同来完成文件在不同客户端之间的传递,下面是 BitTorrent 系统的工作原理:
-
创建种子文件:首先,文件共享者使用一个 BT 客户端软件创建种子文件。种子文件包含了所有需要共享的文件的元数据,包括文件名、大小、哈希值和 tracker 服务器的地址等信息。
-
共享种子文件:文件共享者将种子文件上传到一个或多个 Tracker 服务器上。Tracker 服务器是用于协调 P2P 网络的中心服务器,用于帮助客户端找到其他客户端以共享文件块。
-
下载种子文件:文件下载者下载种子文件并使用 BT 客户端软件打开它。BT 客户端会从种子文件中提取元数据并连接到 Tracker 服务器以获取其他客户端的信息。
-
连接其他客户端:BT 客户端通过 Tracker 服务器找到其他正在共享该文件的客户端,并建立连接以请求文件块。客户端之间的通信是直接的,没有中央服务器,每个客户端都能够共享文件块和请求文件块。
-
请求和共享文件块:BT 客户端请求所需的文件块,并从其他客户端下载和共享它们。BT 客户端将下载的文件块保存在本地硬盘上,并验证它们的哈希值以确保它们的完整性和正确性。
-
共享文件块:当文件下载者的 BT 客户端下载完所有文件块后,它可以选择继续共享这些文件块,以帮助其他客户端更快地下载文件。
2.3.3 BitTorrent 协议
BitTorrent 协议[21]中有关客户端节点与 Tracker 节点的交互协议定义如下:在执行下载任务时,终端需要向 BT Tracker 服务发送一个 Tracker GET 请求,以获取当前正在下载同一资源的对等结点信息。Tracker GET 请求包含如下参数:info_hash(20 字节)、peer_id(终端生成的 20 个字符的唯一标识符)、IP(可选,该终端的 IP 地址)、Port(该终端正在监听的端口)、uploaded(当前已上传的文件字节数)、downloaded(当前已下载的文件字节数)、left(当前仍需要下载的文件字节数)、numwant(可选,希望返回的 peer 数目,默认为 50 个 IP 和 Port)、event(可选,该参数的值可以是 started、completed、stopped、empty 其中之一)。请求成功后,BT Tracker 会返回一个 Bencoding 编码的字典,其中包含警告信息、等待时间、已完成下载的 peer 数量、未完成下载的 peer 数量以及对等结点信息。
不同对等节点之间的通信协议 Peer Protocol 定义如下:在建立完传输层连接(如 TCP)之后,对等节点开始进行 Peer Protocol 的握手。握手消息依次含有如下数据:pstrlen,该值固定为 19;pstr,该值为“BitTorrent protocol”;reserved,保留字段,用于以后扩展用,一般将这 8 字节全部设置为 0。任何一方当收到非法的握手信息应立即断开连接。若校验没有问题,则握手成功,之后对等双方开始进行数据传输。
数据的通用格式为<length prefix><type id><payload>。其中,length prefix 代表消息的长度(即 type id 的长度与 payload 的长度之和),type id(十进制整数)指示消息的类型。特别地,length prefix 为 0 代表 Keep Alive 消息。对于其它类型的消息,其对应的 type id 依次为:0(choke 消息)、1(unchoke 消息)、2(interested 消息)、3(not interested 消息)、4(have 消息)。其中,have 消息的 payload 只包含一个整数,该整数对应的是该终端刚刚接收完成并校验通过 SHA1 哈希的 piece 索引。终端在接收到并校验完一个 piece 后,就向它所知道的所有 peer 都发送 have 消息以宣示它拥有了这个 piece。其它终端接收到 have 消息之后便可以知道对方已经有该 piece 的信息。
2.4 本章小结
本章首先概述了有限域运算的基础知识,介绍了有限域的构造方法,之后介绍了网络编码理论,通过蝴蝶网络论述了网络编码如何有效提高网络吞吐率,之后介绍了 BitTorrent 系统的工作原理,并入分析了 BitTorrent 协议的具体内容。
第三章 编译码算法和改进型 BT 系统的设计与实现
本章将首先讨论为什么要选择 GF(256)作为网络编码编译码过程的有限域基础,并介绍有限域算法的实现方法;之后介绍对网络编码编译码算法的分析以及相关的算法优化方案,包含稀疏编码、分代编码、启发式编码以及对高斯约旦消元算法的并行优化设计和数据包的线性检测。
最后介绍将网络编码应用到分布式文件传输中的改进型 BitTorrent 系统 PeerCodeX 的设计方案,包括种子文件设计、分布式节点间协议设计和系统的概要设计。
3.1 有限域运算算法
3.1.1 有限域的选择
网络编码中需要将数据分成块,并通过系数向量的乘法来计算编码向量。为了解码,客户端需要收到足够多的线性无关的系数向量和编码向量。如果不使用有限域的运算规则,矩阵相乘会导致数据位数增加和数据字节长度不确定性。在无限域上,涉及除法运算,需要转换成浮点数形式,无法保证正确性,且科学计算增加了复杂度,因此应使用有限域运算。 在构造有限域时,需要考虑数据计算时最小计算的单位元素的位数和及其表示的数值大小。然而,在素数域中按照固定的位大小来计算数据,过小的域空间可能无法涵盖所有的数据,而过大的域空间则可能导致计算后的结果超出原有数据的表示范围。因此,使用素数域可能并不是一个理想的选择。 接下来将讨论如何确定有限域 GF(p^n)中 p 与 n 的取值。有限域在 GF(2)上的运算规则有以下特殊性质:
表 3.1 GF(2)上的运算规则
| + | 0 | 1 | - | 0 | 1 | × | 0 | 1 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
在计算机中,GF(2)的加法和减法可以采用异或操作,而乘法运算可以采用和操作,因为底层的指令支持,可以极大地提高运算速度,所以 p 的取值为 2。 在网络编码中,传输的数据包包含系数向量和编码向量。由于编码向量与原始数据大小相同,过大的系数向量会造成网络流量的浪费,降低信息密度。此外,当有限域的大小增加时,计算所需的资源也会增加。因此,在实际应用中,通常采用较小的有限域来进行网络编码。这样可以节省网络资源,并提高信息传输的效率。但如果有限域太小如 GF(2^3),则无法产生足够多的线性无关的编码向量,因此在解码时将需要更多的数据包,这样不仅会消耗更多的网络流量,同时还会导致计算资源的浪费。在计算机中,数据都是以 8 位/一个字节为单位存储和传输的,所以采用 GF(2^8)可以更好地实现与计算机领域相结合,并且有较低的线性相关概率。
3.1.2 有限域算法的实现
考虑 $GF(2^{8})$ 上多项式的加法和减法运算,因为二元组就是 01 序列,n 元组 $(a_{n-1}, …, a_{1}, a_{0})$ 就是 n 比特长度的 01 序列,其可以表示为多项式
$f(x)=a_{n-1}x^{n-1} + … + a_{1}x + a_{0} = \sum_{i=0}^{n}a_{i}x^{i} \quad \forall i \in \lbrace 0, 1, 2, …, n-1 \rbrace, a_{i} \in \lbrace 0, 1 \rbrace$ (3-1)
的形式,比如 01010111 其可以表示为 $f(x) = x^{6} + x^{4} + x^{2} + x + 1$,因此有限域 $GF(2^{8})$ 上的运算可以转换为多项式的运算。
对于多项式 $f(x) = x^{6} + x^{4} + x^{2} + x + 1, g(x) = x^{7} + x + 1$,其加法运算过程如下:
$f(x) + g(x) = (x^{6} + x^{4} + x^{2} + x + 1) + (x^{7} + x + 1) = x^{7} + x^{6} + x^{4} + x^{2}$ (3-2)
转换到二进制的角度,其运算过程相当于异或运算:
$(01010111) \bigotimes (10000011) = 11010100$ (3-3)
生成元的幂可以遍历域上的所有元素。假设 $g$ 是域 $GF(x^{n})$ 上生成元,那么集合 $ \lbrace g^{0}, g^{1}, …, g^{2n-1} \rbrace$ 就包含了域 $GF(x^{n})$ 上所有非零元素。
将生成元应用到多项式中, $GF(x^{n})$ 中的所有多项式都是可以通过生成元 $g$ 求幂得。即域中的任意元素 $a$ ,都可以表示为 $a = g^{k}$。
$GF(x^{n})$ 是一个有限域,就是元素个数是有限的,但指数 $k$ 是可以无穷的。所以必然存在循环。这个循环的周期是 $2^{n} -1$ ( $g$ 不能生成多项式 $0$)。所以当 $k$ 大于等于 $2^{n} -1$ 时,$g^{k}=g^{k \% (2w-1)}$。
对于乘法,假设 $a = g^{n}$,$b = g^{m}$。那么$ab = g^{n}g^{m} = g^{n+m}$。那么可以使用查表的方法,根据 $a$ 和 $b$,分别查表得到 $n$ 和 $m$,然后查表 $g^{n+m}$ 即可。
下面介绍既约多项式的概念,若域 F 中多项式 $f(x)$ 不能表示域 F 上任两个多项式$g_{1}(x)$ 和 $g_{2}(x)$ 的乘积 $g_{1}(x)$ 和 $g_{2}(x)$ 在域 F 中,且次数都小于 $f(x)$ 的次数,那么称多项式 $f(x)$ 为既约多项式,在有限域运算中可以作为乘法运算中的模。
实现中选择 $x^{8} + x^{4} + x^{3} + x^{2} + 1$ 作为既约多项式,2 作为生成元,在使用之前生成指数表和对数表,算法如下:
# 算法1:生成指数表和对数表
# - 输入:有限域元素数量 n,生成元 g,既可约多项式 p。输出:指数表 exp 和对数表 log
# - 声明并初始化 x 为 1
for i 从 0 到 n – 2 do
if x == 1 并且 i != 0 then
抛出异常
end if
exp[i] ← x
exp[i+n-1] ← x
log[x] ← i
x 重新赋值为 x 和 g 的乘积
end for
其中为了简化乘法运算加倍 exp 表。其中使用到的有限域乘法如下:
# 算法2:有限域乘法
# - 输入:乘数 x,y;既可约多项式 poly;有限域维度 k。输出:乘法结果
# - 声明并初始化结果 z 为 0
for i 从 0 到 k – 1 do
if y 的最后一位是1 then
z ← z 异或 x
end if
x 左移 1 位
y 右移 1 位
if x 的最高位是1 then
x ← x 异或 poly
end if
end for
3.2 网络编码改进型编码译码算法研究
3.2.1 编码算法的设计与优化
-
随机线性网络编码
随机线性网络编码(Random Linear Network Coding)可以在分布式传输中提高数据传输的可靠性和效率。该技术利用线性代数的原理,在网络节点之间随机生成线性组合的编码包,然后将它们发送到其他分布式节点。分布式节点可以通过收集足够数量的线性无关的编码包来恢复原始数据。随机线性网络编码的突出特点是每个分布式节点不需要知道整个网络的拓扑结构,在没有足够多的先验知识的情况下,只需要通过生成随机系数来计算编码包即可在保证全局的最优性,这种特性使得其可以应用在网络结构持续变化的分布式文件共享系统中。
网络编码中的编码数据包具有高信息熵和等价性,使得每个节点都能以较低的成本获取足够的线性无关编码数据包来解码原始文件。在 BitTorrent 系统中,每个 piece 大小一般为 256KB,1G 文件包含 4096 个 piece。如果某些节点退出,导致一个 piece 消失,网络中所有节点都将无法完成下载。
图 3.1 展示了基于 P2P 文件共享系统中网络编码的应用方式。Client A 向 client B 发送的是编码数据包,client B 向 client C 发送的是重新编码的数据包。Client A 的数据分组为 $M = (M_{1}, …, M_{n})$,选取有限域 $GF(2^{8})$ 上的系数向量 $C = (c_{1}, …, c_{n})$,其中数据分量均为有限域上的随机数,编码过程为系数向量 $C$ 和数据向量 $M$ 的矩阵乘法,数据分量之间的运算采用有限域计算的方式,即数据向量的每个数据分量的每个字节与系数向量的数据分量单独计算,最终得到编码向量 $N$,Client B 在接收到足够多的线性无关的向量之后即可解码原始数据。
当 client B 在尚未解码完成时,可以通过对编码数据包进行重新编码生成新的编码数据包提供给 client C。当 client B 已经接收并存储了一组编码数据包时,其可以在有限域 $GF(2^{8})$ 上选择一组向量 $H^{'} = (h_{1}^{'}, …, h_{k}^{'})$,通过矩阵 $(C_{1}, …, C_{k})^{T}$ 与 $H^{'}$ 的矩阵乘积获取新的系数向量 $C^{'}$,而编码矩阵 $(N_{1}, …, N_{k})^{T}$ 与向量 $H^{'}$ 的乘积可以得到新的编码向量。
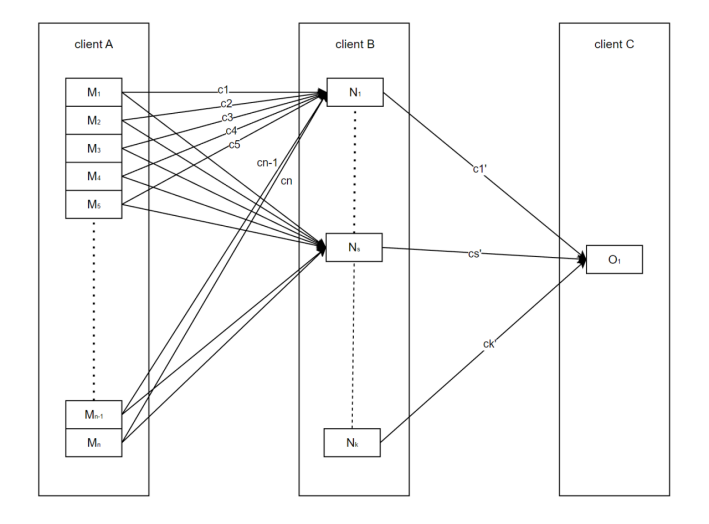
图 3.1 随机线性编码技术在 P2P 文件共享系统中的应用原理图
-
稀疏编码
尽管随机线性网络编码解决了将网络编码应用于分布式文件共享系统的可行性问题,但由于其高计算复杂度和内存占用较高,它在解决系统可用性问题方面并不高效。尽管消费级个人电脑的性能和内存不断提高,但网络带宽也在提升,全编码的随机线性网络编码算法在编码和解码性能方面依旧无法满足普通用户分享文件时对编译码速率的需求。
相比之下,稀疏编码能够在保证编码数据包拥有足够的信息熵和较低的线性相关性的前提下,减少信息处理次数,提高编译码效率。
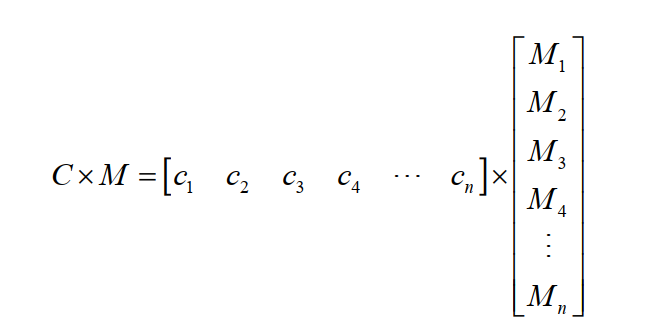 (3-4)
(3-4)公式 3-4 中是一个编码数据包生成过程。如果采用稀疏编码,则系数向量 $C$ 中将含有较多的 0 元素,其在矩阵计算过程中可以直接跳过该分量的计算步骤,这样可以大幅降低计算复杂度,在 4.2 节中将看到稀疏编码对编码性能提升的贡献。同时通过测试可知,稀疏度越高,编码速度越快。
在解码算法中,稀疏编码同样可以大幅提升解码器性能,将在解码算法章节介绍稀疏编码如何降低解码复杂度。
-
分代编码
传统网络编码在计算编码数据包时,是将数据文件的整体分块计算编码向量,该方法在面临用户传输文件的大小下至 100M 上至 100G 的宽范围文件大小时,显现出力不足信的情况。
若将 100GB 的文件整体分块计算,将会带来极大的计算资源开销,这种情况不是普通消费级设备可以承受的。同时,若每个分块的大小过大,会导致每个编码数据包的大小也过大,在网络传输中会降低网络传输效率,过长的传输时间还容易受网络波动的影响导致传输失败,进而降低传输网络的健壮性。但如果每个分块的大小过小,则需要更大的系数向量。由于数据文件非常大,系数向量在编码数据包中的占比将很大,这又会降低网络带宽利用率。同时,过大的稀疏矩阵同样会提高解码复杂度。
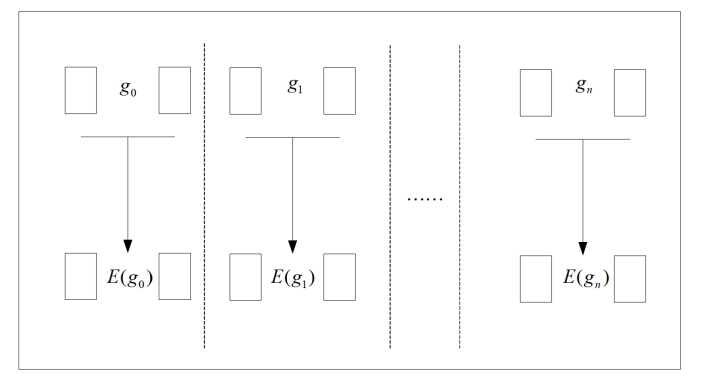
图 3.2 分代网络编码
分代编码是指将文件分成多个代际,每个代际作为一个单独的单位进行分块和网络编码,各个编码之间是相互独立的,如图 3.2 所示。这种分代设计可以大幅降低编码和解码复杂度,4.4 节中的测试说明分代大小并不会影响解码复杂度。尽管分代算法将整个文件分成多个代际,但相较于 BitTorrent 系统中每 piece 仅 256KB 的情况,本算法采用每个分代 128MB、每块 1M 的算法,在分代大小上有多个数量级上的差距,因此不会有 BitTorrent 中系数块的问题。
3.2.2 解码算法的设计与优化
-
高斯约旦消元法
高斯约旦消元法是一种通用的线性代数计算方法,其解码速度也许不是最快的,但在网络编码的解码中是最合适的。
高斯约旦消元法将线性方程组转化为简化的上三角矩阵,之后再转化为稀疏矩阵为单位矩阵,只要系数矩阵能转变为单位矩阵,则解码成功。如公式 3-5 所示,首先,将线性方程组写成增广矩阵的形式。
 (3-5)
(3-5)接下来,选取矩阵中第 $k$ 列中的最大值作为主元,将该主元所在行与第 $k$ 行交换,确保主元在第 $k$ 行上。然后,将选定主元的第 $k$ 行消元,使其它行中的第 $k$ 列系数为零。重复上述步骤,将第 $k+1$ 行作为下一次循环的主行,直到将整个矩阵转化为简化的上三角矩阵。
之后进行回代过程,将上三角的非零元素置零。从矩阵的最后一行开始,依次求解未知数的值。具体来说,对于第 $i$ 行的未知数,需要将其右侧系数已知的未知数值代入方程中,并求解第 $i$ 个未知数。从下至上依次求解出所有未知数的值,并且将该位置的系数分量置为 1,从而得到解的向量。
这个过程结束后,将所有元素为 0 的横向分量从增广矩阵中移除,这是因为线性方程组中存在线性相关的方程,在高斯约旦消元后因为矩阵的秩不变从而产生了全零分量。
上文提出的稀疏编码可以有效降低高斯约旦消元法的计算复杂度,在计算上三角矩阵的过程中,如果第 $k$ 列中新向量的分量为 0 则可以直接省略此列的消元过程,稀疏度越高,消元时所需的计算就越少,同时,回代过程中将上三角的非零元素置零的过程与消元过程类似,同列的每个零元素都可以减少一次行变换,稀疏度越高,所有列中的零元素就越多,可以将行变换的次数降低从而降低算法的计算复杂度。
该算法具有原地解码的能力,不需要请求更多的内存,从而尽可能地减少了解码过程中的内存占用。此外,该算法解码效率稳定,不会因为稀疏编码带来的不确定性而产生性能波动。由于其独特的解码过程,该算法可以实现渐进式解码。具体来说,分布式节点可以每获取到一个编码数据包就将其放入解码器进行解码,即将编码数据包作为一个横向分量放入增广矩阵的最下方,并进行求解步骤。这种算法能够边下载边解码,有效地在时间上分摊了解码时的计算过程,提高了计算资源的利用率。
-
线性相关检测
线性相关检测是一种在编码数据包放入增广矩阵之前检测其是否与已有数据包线性相关的操作。如果线性相关,该数据包将不会加入增广矩阵中进行解码。这种操作可以降低解码复杂度,因为所选择的分代分块大小极大地降低了线性检测的复杂度。在每个分代 128MB、每块 1M 的情况下,稀疏矩阵的最大大小为 128*128 字节矩阵,这种大小对计算机的计算强度要求非常小。因此,只需将已有增广矩阵的系数部分复制一份,并将新数据包的系数向量加入矩阵中,然后对这个极小的矩阵进行一次高斯约旦消元,即可检测新数据包的线性相关性。在每个编码向量为 $2^{20}$ 字节的情况下,单独检测线性相关性可以有效减少计算资源的消耗,同时线性相关检测可以识别出网络中的相似节点,减少不必要的线性相关数据包的传输,提高分布式网络的效率。
-
多线程优化
在高斯约旦消元时,列主元消元法需要将其他行的系数变为零。此时,不同行的计算过程不会发生写冲突,因此可以采用并行计算的方式来加速该过程,充分利用多核 CPU 的优势。同时,在回代过程中,可以并行化解决将已知元素上方的元素解为零的任务。根据第 4.5 节的测试结果表明,采用并行计算可以显著提高解码速度,并行计算优化过的算法相较于传统算法有 3 至 4 倍的性能提升。在当前的网络环境下,这种加速已经足够满足日常使用的需求。
3.3 改进型 BitTorrent 系统的设计
3.3.1 种子文件设计
在应用网络编码前,需要对种子文件进行一些必要的修改,以适应新的系统环境。基于本文 2.3.1 节中所描述的种子文件,进行了如下的调整和更新:
由于取消了 Tracker 服务器的设置,需要将 announce 和 announce-list 记录的对等节点地址改为由发布者提供的地址。同时,在 Info 字段中,取消了 piece length 字段,而将 Piece 字段改为 Hash 列表字段,并记录了每个分代数据的 SHA1 哈希值。这样,可以更有效地实现数据的传输和处理。
此外,文件编码格式仍采用 Bencoding 编码,但拓展名已改为“.nc”,以便更好地于 BitTorrent 系统区分。
3.3.2 分布式节点间协议设计
为使系统更稳定,同时降低系统的实现难度,对 BitTorrent 协议进行了简化,同时可以更好地引入上文论述的网络编码算法,更好地满足 P2P 网络中的文件共享需求。
为了提高网络的健壮性,更好地发挥分布式网络的优势,取消了 Tracker 服务器,分布式节点通过直接向邻居节点发送请求来获取更多的邻居节点,所以废弃了分布式节点与 Tracker 服务器之间的通信协议,将其承担的功能放入分布式节点之间的通信协议中。
首先对握手协议进行修改。对等结点在建立完传输层 TCP 连接之后,便开始进行 Network Coding 的握手,握手消息依次含有如下数据:
-
pstrlen, 该值固定为 14 ,大小为 1 个字节
-
pstr, 该值为 “Network Coding” (新协议的关键字)
-
reserved, BT 协议的保留字段, 8 个字节,这里拓展使用
-
info_hash, 种子文件中分代数据的哈希,20 个字节
-
server_port, 分布式节点向其他节点提供服务的端口,大小 2 个字节,使用大端序
对等节点一方在传输层连接建立以后便发送握手信息,另一方收到握手信息后也回复一个握手信息,如果任何一方收到了非法的握手信息,都会立即中断连接。如果分布式节点中没有 info_hash 表示的分代数据,则其返回的握手信息中 info_hash 字段全为 0,在发送完握手信息后即可中断连接。
这里 reserved 字段的数据决定了这个连接的目的。对于心跳连接,reserved 字段的第一个字节为 0x01,其余均为 0,对等节点在发送并接收到握手信息后即可断开连接。
对于获取邻居节点信息的连接,reserved 字段中第二个字节为 0x01,其余全为 0,握手信息发送完后,被请求方则发送邻居节点的数据,之后双方可断开连接。邻居节点数据包的数据格式如下:
-
type,数据包类型,邻居节点的数据包类型为 0x01,一个字节
-
strlen,之后 data 数据的字节数,大小为 4 个字节,使用大端序
-
data,邻居节点的数据,格式为以逗号分隔的地址,地址格式为 host:port
如果连接是请求编码数据,则 reserved 第三个字节为 0x01,其余字节均为 0,握手成功后,数据提供节点即可持续发送编码数据,数据包格式如下:
-
type,数据包类型,编码数据的数据包类型为 0x02,一个字节
-
vector_len,系数向量大小,8 个字节,使用大端序
-
vector,系数向量列表
-
coded_vector_len,编码向量大小,8 个字节,使用大端序
-
coded_vector,编码向量
3.3.3 PeerCodeX 系统设计
上文研究和分析了 BitTorrent 系统的工作原理并设计了网络编码算法,这里将网络编码技术应用到 BitTorrent 系统中,设计出一种基于随机线性网络编码的文件共享系统——PeerCodeX。该系统旨在解决 BitTorrent 系统在应用中所遇到的问题,弥补其不足之处。PeerCodeX 系统充分利用了网络编码技术和当前 BitTorrent 协议的分布式优势,以实现更好的文件传输效果。
PeerCodeX 采用完全分布式设计,取消了 Tracker 服务器,Tracker 服务器的邻居节点发现功能由分布式节点支持。用户可使用 PeerCodeX 创建种子文件,之后将种子文件通过互联网分享给他人,用户通过 PeerCodeX 开启文件上传服务,通过监听特定端口向其他节点提供服务。PeerCodeX 使用 go 编写,可以利用该语言优秀的 goroutine 设计,同时保证性能;UI 采用 fyne 包实现。
PeerCodeX 通过添加种子文件,可以查看种子文件的信息,如 announce,comment 等,如果本地没有原文件,则可以向 announce 设置的地址发起 TCP 连接请求系数向量和编码向量,PeerCodeX 请求时,遵照上一节网络编码协议的设计,请求特定分代的数据,并使用 3.2 节设计的解码算法实现的的解码器对接收到的数据进行渐进式解码,即每收到一个编码数据包就将其输入到解码器解码,同时将编码数据包输入到重编码器以向其他节点提供数据包,在特定分代的数据解码完成并通过计算数据哈希验证数据正确性后,即可将解码后的数据按照分代位置写入硬盘中文件的指定偏移地址并关闭解码器,之后移除重编码器,同时不再向其他对等节点请求本代的系数向量和编码向量。如果其他节点继续向本节点请求该分代的数据包,则从文件中读取该分代的数据以创建新的编码器为其他节点提供服务。在所有分代都解码成功并写入文件后即可获得完整的原始文件。
为了更好地实现 PeerCodeX 的功能,将其分为六个模块:编码器模块、客户端模块、服务端模块、数据中心模块、种子文件管理模块,UI 交互模块。图 3.3 是基于随机线性网络编码的 PeerCodeX 的模块图。
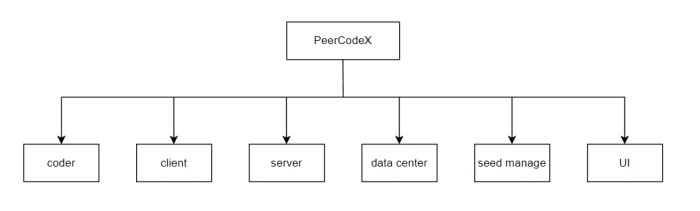
图 3.3 PeerCodeX 模块图
-
coder 模块
coder 模块负责数据的编码、重编码和解码,编码器采用启发式线性随机稀疏网络编码算法编码;重编码器接收编码数据,在本代数据解码过程中负责向其他节点提供编码数据包;解码器使用 goroutine 实现并行计算。
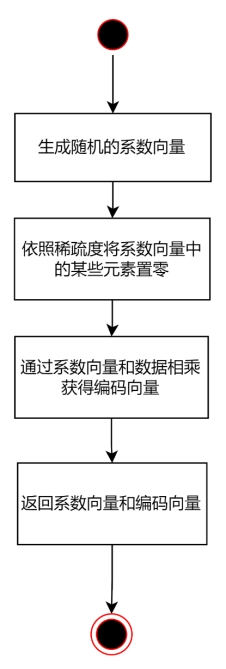
图 3.4 编码过程
图 3.4 展示了随即线性稀疏编码器的编码过程。
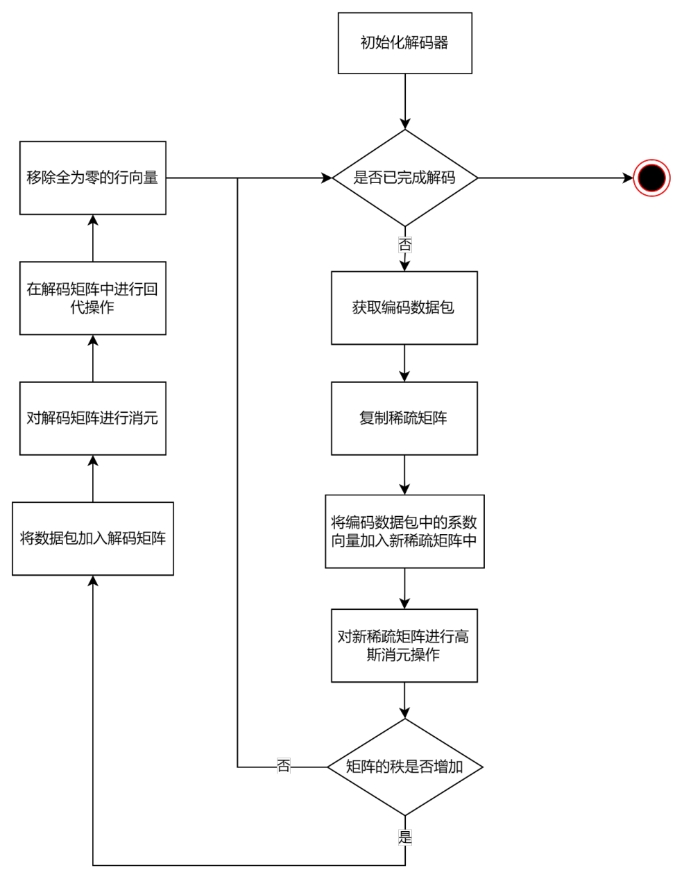
图 3.5 解码过程
图 3.5 展示了加入线性相关性检测模块的高斯消元法的解码过程。
-
client 模块
client 模块负责所有向其他分布式节点发送网络请求的任务,如获取编码数据包、获取邻居节点、检测节点状态等。client 启动多个定时器用以更新程序状态,第一个计时器按照指定频率通过发送心跳连接检测一次 data center 中保存的对等节点状态;第二个计时器根据 data center 中记录的最大连接数配置动态调整当前获取编码数据包的 goroutine 客户端数目;第三个是计时器则根据 data center 中活跃的对等节点数目调整邻居节点数量,如果可提供编码数据包的邻居节点数量不满足解码需求,则向当前提供编码数据包的节点发送邻居节点请求,并将结果保存到 data center 模块中。
-
server 模块
server 模块负责向对等节点提供心跳检测、邻居节点、编码数据包服务。每获得一个新的连接就启动一个 goroutine 提供服务,根据握手信息提供给相应的数据,邻居节点信息和编码数据包都从 data center 获取。
-
data center 模块
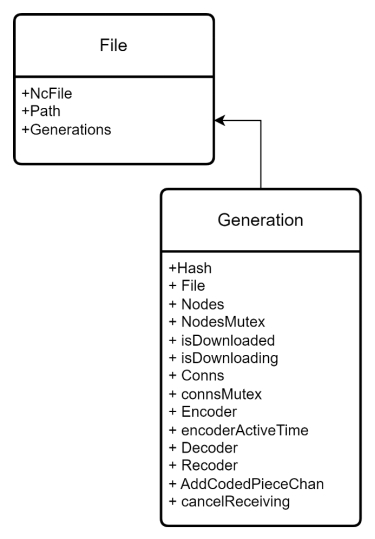
图 3.6 data center 类图
data center 模块是 PeerCodeX 的核心模块,其保存有应用的配置信息,同样维护着文件列表,每个文件都有其对应的种子文件,种子文件的每个分代都有其可选的对应的编码器、重编码器、解码器以及保存着请求编码数据包的 TCP 连接,每个文件都有其可以提供服务的节点列表,图 3.6 展示了 data center 模块的类图。
-
seed manage 模块
seed manage 模块负责种子文件的创建和解析。
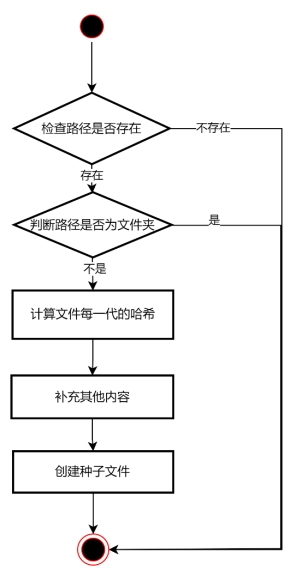
图 3.7 创建种子文件流程图
图 3.7 展示了创建种子文件的流程图。
-
UI 模块
UI 模块负责与用户交互,包括设置配置、启动服务、创建种子文件、下载文件。
3.4 本章小结
本章最先介绍了有限域的选择以及有限域算法的实现,为网络编码提供计算支持。之后介绍了启发式随机线性稀疏编码算法和多线程优化的高斯约旦消元法,并介绍了线性检测模块的设计方案。最后介绍了改进型 BitTorrent 系统的种子文件设计、分布式节点间协议设计以及原型系统 PeerCodeX 的设计方案。
第四章 编译码算法及改进型 BT 系统的实验分析
本章将通过不同维度的测试来支持第三章中讲述的网络编码算法相对于传统算法的优势,同时通过测试结果来佐证第三章中编译码算法的设计方案。
4.1 实验环境
实验使用的设备为惠普的消费级笔记本,型号为 OMEN15-dc1055TX,CPU 型号为 Intel(R) Core(TM) i5-8300H CPU @ 2.30GHz,系统内存为 32GB,操作系统为 64 位的 Windows 11 专业版,版本号为 22H2/ 22621.1555。使用 Windows Subsystem for Linux 的 Debian 系统作为实验平台,WSL 版本为 1.2.5.0,内核版本为 5.15.90.1-microsoft-standard-WSL2。
4.2 稀疏编码的稀疏度对编码解码的影响
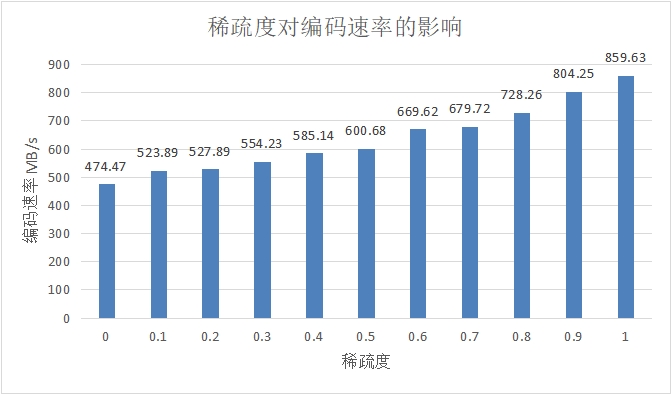
图 4.1 稀疏度对编码速率的影响
图 4.1 中以 128MB 数据,128 个分块为例,展示了稀疏度对编码速率的影响。实现表明,稀疏度越高,零元素的数量就越高,计算时就能减少更多的乘积和求和运算,编码速率也越高,但稀疏度过高同样会带来线性相关的问题,如稀疏度为 1 时解码速率最高,但此时完全无法实现解码操作,因此需要通过对解码器进行试验,确认合适的稀疏度。
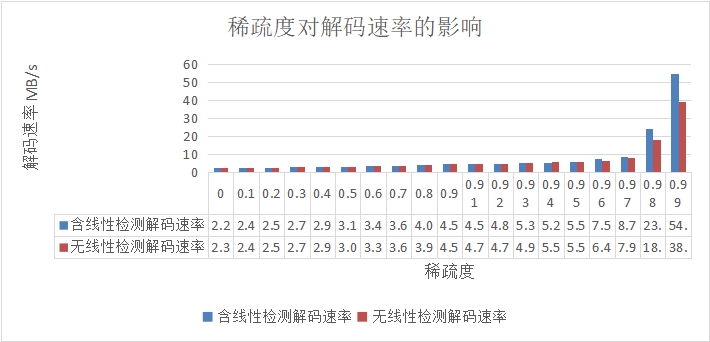
图 4.2 稀疏度对解码速率的影响
图 4.2 中是以 128MB 数据,128 个分块为例,展示了不同稀疏度对解码速率的影响,实验可知,稀疏度越高,解码速率越快,但稀疏度高同样会带来线性相关的问题,解码时需要更多的数据包,这会占用更多的网络带宽。在图 4.2 中同样测试了线性检测模块对解码速率的影响,可知,在稀疏度低时,因为数据包的线性相关度高,线性检测只会增加解码复杂度,但在稀疏度高时,线性检测可以显著提高解码速率,避免线性相关数据包降低解码速率,同时线性检测在网络中可以避免线性相关数据包的传播,因为线性相关检测对线性无关数据包的解码速率影响较小,总体上线性检测具有优势。
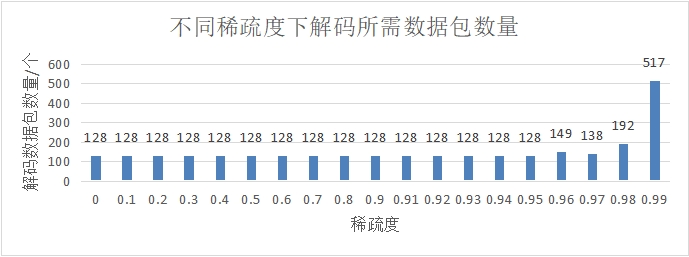
图 4.3 不同稀疏度下解码所需数据包数量
图 4.3 中展示了不同稀疏度下解码所需数据包数量,可知在稀疏度过大时,数据包由于编码使用的数据块过少导致产生了线性相关的数据包,因此在解码时需要更多的编码数据包参与解码工作,这降低了网络利用率。其中在稀疏度为 0.95 时,保证了既不增加线性相关性又能提高解码速率,因此方案以 0.95 作为最佳稀疏度。
4.3 分块数量对编解码速率的影响
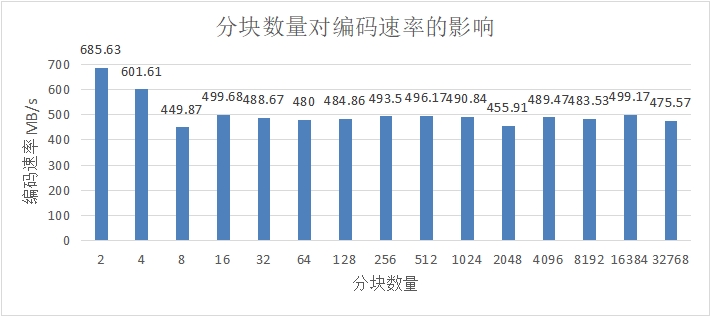
图 4.4 分块数量对编码速率的影响
图 4.4 以 128MB 数据为例,采用线性随机网络编码,展示了不同分块数量对编码速率的影响,除了分块为 2 和分块为 4 的两种情况下编码速率会有比较优势外,选择其他分块数量对编码速率无显著差异,但如果选择的分块数量过少,那么编码数据包会过大,在传输过程中遇到网络波动会使得编码数据包传输失败,选择小的编码数据包可以更好地应对网络的不稳定性,提高网络利用率,因此应当选择合适大小的分块数量。
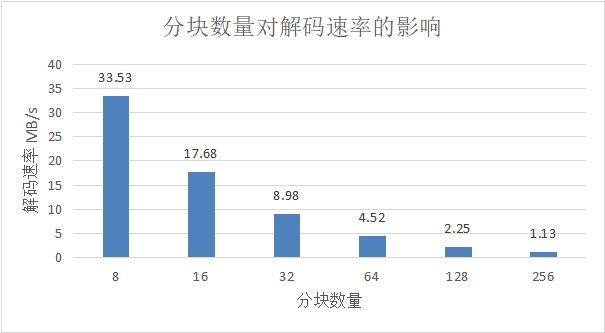
图 4.5 分块数量对解码速率的影响
图 4.5 以 128MB 为例,展示了不同分块数量对解码速率的影响,通过实验可知,分块数量与解码速率成反比关系。在网络编码中,分块数量越多,编码向量的线性相关性越低,每个编码数据包的大小也越小,更不易受网络波动的影响,在保持足够高解码效率的情况下,选择 128 作为编译码的分块数量。
4.4 代际大小对编解码速率的影响
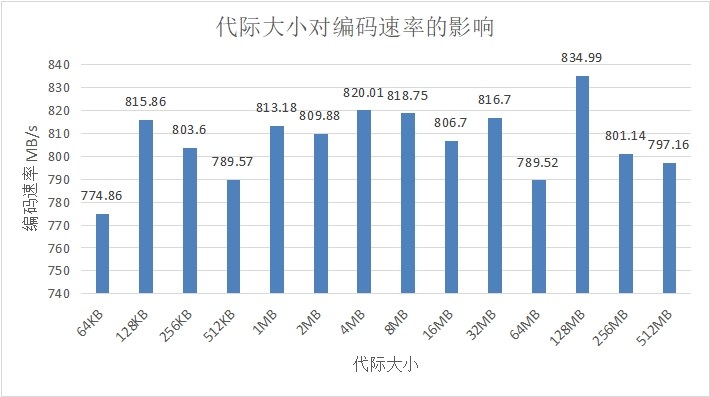
图 4.6 代际大小对编码速率的影响
图 4.6 以 128 个分块,稀疏度为 0.95 为例,展示了代际大小对编码速率的影响,由图 4.6 可知,编码速率与代际大小无显著相关性。
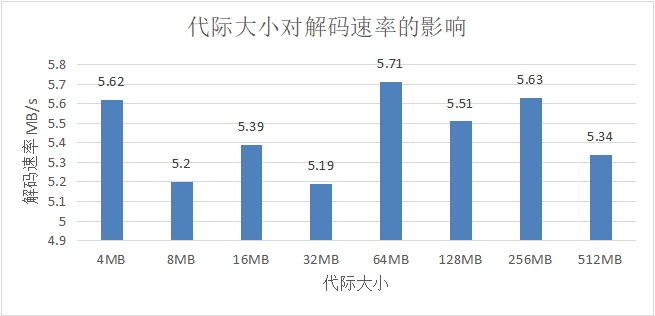
图 4.7 代际大小对解码速率的影响
图 4.7 以 128 个分块,稀疏度为 0.95 为例,展示了代际大小对解码速率的影响,实验表明,代际大小不影响编码速率。
4.5 并行解码算法对性能的影响
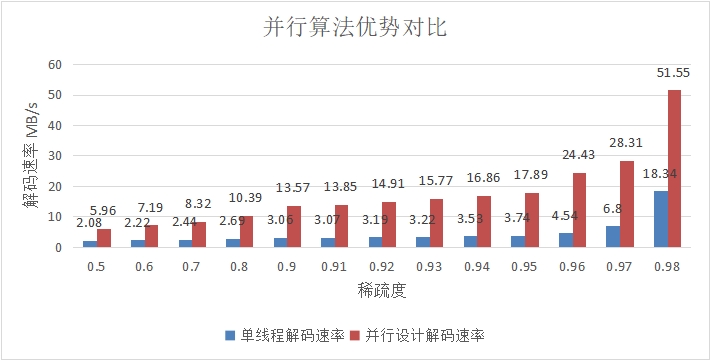
图 4.8 并行算法优势对比
图 4.8 展示了不同稀疏度情况下单线程算法与并行算法的速率对比,实验表明,对高斯约旦消元法的消元和回代过程的并行化计算可以大幅提高解码效率。
4.6 本章小结
经过测试可知目前的多种算法优化方案可以显著提高 P2P 文件共享系统中网络编码的解码速率。这些优化方案可以有效地提高文件传输的效率和可靠性,从而为用户提供更好的使用体验。
第五章 总结与展望
本章旨在概述全文内容,总结网络编码算法的相关研究工作,并指出所提出的启发式随机线性稀疏网络编码算法和多线程优化的高斯约旦消元译码算法存在的不足之处以及可改进的空间。同时将展望未来的研究方向。
5.1 总结
网络编码应用于 P2P 文件共享系统中是一种新颖的设计方案,其可以解决现有 BitTorrent 系统文件块选择算法只能达到局部最优以及对网络带宽利用率不高的问题。但因为随机线性网络编码有较高的编译码复杂度,其在实际应用中,并不能发挥出应有的优势。本文针对这一问题,对网络编码的编译码算法进行了研究,提出了启发式随机线性稀疏网络编码算法。
本文主要完成了如下工作:
-
介绍了有限域运算的基础知识和基本概念,以及有限域构造的方法。同时,探讨了网络编码理论的提出及其在网络传输中的优势,并深入分析了 BitTorrent 系统的设计方案和协议。
-
阐述了有限域选择问题,并通过对有限域运算的分析,设计并实现了相应的有限域运算算法。
-
分析并实现了随机线性稀疏网络编码算法,并通过实验确定了最佳的稀疏度。此外,还选择了最佳的分代大小和分块大小,并对高斯约旦消元算法进行了优化,以降低线性相关编码对计算资源的消耗。通过并行设计,有效降低了译码算法的译码时间。
设计并实现了基于本文提出的网络编码的编译码算法和改进型 BitTorrent 协议的分布式文件共享系统演示系统 PeerCodeX。
5.2 本文展望
本文虽然通过算法的改进做出了可以实用的原型系统,但在算法的设计和系统功能上仍有较大的改进空间,有以下几个方向:
-
将有限域空间从 $GF(2^{8})$ 扩展到 $GF(2^{64})$ 有效提升 64 位操作系统的优势,降低编译码复杂度,同时设计专用的有限域硬件运算器,解决查表法内存占用高的问题。
-
考虑将编译码过程和有限域运算过程结合起来,设计更高效的算法,尝试将运算从整体上并行化和流水线化,利用 GPU 加速的优势,提高编译码效率。
-
优化协议设计,加入更多分布式节点间通信功能,增加分布式节点的先验知识,设计新的环路检测机制和编码方案,使分布式节点可以获取更多线性无关的编码数据包,考虑降低网络连接次数,提高网络效率。
-
优化原型系统 PeerCodeX 的内存占用,灵活调整解码器的内存占用,包括将较长时间无法解码的译码器的数据存入硬盘降低内存占用,依据系统内存使用情况,动态调整译码器数量。
参考文献
[1] Krishnamurthy, B., & Wills, C. (2001). Content distribution networks: An overview of research issues. IEEE Internet Computing, 5(4), 36-44.
[2] Tom Strickx, Jeremy Hartman. Cloudflare outage on June 21, 2022[EB/OL]. [2023-4-21]. https://blog.cloudflare.com/cloudflare-outage-on-june-21-2022/.
[3] Cohen, B. (2003). Incentives Build Robustness in BitTorrent. In Proceedings of the 1st Workshop on Economics of Peer-to-Peer Systems (pp. 68-72). Berkeley, CA, USA: ACM Press.
[4] Guo, J., Chen, S., Xiao, L., & Leung, V. C. (2005). Can internet video-on-demand be profitable?. IEEE/ACM Transactions on Networking, 13(3), 427-440.
[5] Ahlswede, R., Cai, N., Li, S. Y. R., & Yeung, R. W. (2000). Network information flow. IEEE Transactions on Information Theory, 46(4), 1204-1216.
[6] Gkantsidis, C., Rodriguez, P. R., & Huitema, C. (2005). Network coding for large scale content distribution. INFOCOM 2005. 24th Annual Joint Conference of the IEEE Computer and Communications Societies. Proceedings IEEE.
[7] Li, S.-Y. R., Yeung, R. W., & Cai, N. (2003). Linear network coding. IEEE Transactions on Information Theory, 49(2), 371-381.
[8] T. Ho, M. Medard, R. Koetter. (2006). A random linear network coding approach to multicast. IEEE Transactions on Information Theory, 52(10), 4413-4430.
[9] Koetter, R., & Médard, M. (2003). An algebraic approach to network coding. IEEE/ACM Transactions on Networking, 11(5), 782-795.
[10] Lun, D. S., Ratnakar, N., Médard, M. (2006). Minimum-cost multicast over coded packet networks. IEEE Transactions on Information Theory, 52(6), 2608-2623.
[11] Patrik J. Braun, Péter Ekler, Frank H. P. Fitzek, Médard, M. (2017). Demonstration of a P2P assisted video streaming with WebRTC and network coding. 2017 14th IEEE Annual Consumer Communications & Networking Conference.
[12] 朱华.(2009).网络编码在 P2P 流媒体点播系统中的应用研究.硕士电子期刊, 2010(02).
[13] 杨军, 戴彬, 黄本雄.(2011).基于网络编码的分层 P2P 网络的拓扑感知算法研究. 计算机工程与科学. 2011,33(02).
[14] 王玉贵.(2012). P2P 内容分发系统中基于信任的网络编码算法研究.硕士电子期刊, 2012(02).
[15] 崔来中.(2013).互联网海量流媒体 P2P 传送性能优化研究.博士电子期刊, 2013(07).
[16] Lidl, R., & Niederreiter, H. (1997). Finite fields. Cambridge, UK: Cambridge University Press.
[17] Joyner, D. (1998). Cryptography and Coding Theory. Springer.
[18] Fragouli, C., Le Boudec, J. Y., & Widmer, J. (2006). Network Coding: An Instant Primer. LCA-REPORT-2005-010. EPFL - IC.
[19] Ford, L. R., & Fulkerson, D. R. (1956). Maximal flow through a network. Canadian Journal of Mathematics, 8(2), 399-404.
[20] Benjamin Fields. (2006). The BitTorrent Protocol Specification. Retrieved from https://www.bittorrent.org/beps/bep_0003.html#bencoding.
[21] Cohen, B. (2003). Incentives Build Robustness in BitTorrent. Proceedings of the 1st Workshop on Economics of Peer-to-Peer Systems. Available online: https://www.bittorrent.org/bittorrentecon.pdf