最近公共祖先lca
含义
对于有根树 T 的两个结点 u、v,最近公共祖先 LCA(T,u,v)表示一个结点 x,满足 x 是 u 和 v 的祖先且 x 的深度尽可能大。在这里,一个节点也可以是它自己的祖先。
算法思路
下图所示:
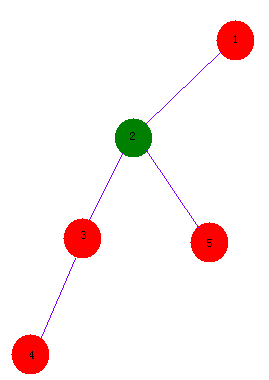
4 和 5 的 LCA 就是 2,那怎么求呢?
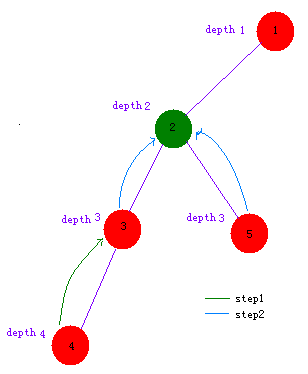
最粗暴的方法就是先 dfs 一次,处理出每个点的深度,然后把深度更深的那一个点(4)一个点地一个点地往上跳,直到到某个点(3)和另外那个点(5)的深度一样然后两个点一起一个点地一个点地往上跳,直到到某个点(就是最近公共祖先)两点“变”成了一个点。
不过有没有发现一个点地一个点地跳很浪费时间?如果一下子跳到目标点内存又可能不支持,因此相对来说倍增的性价比算是很高的。
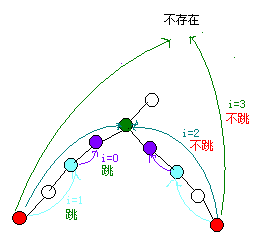
倍增的话就是一次跳 2i 个点,倍增找 lca 的方法是这样的:
从最大可以跳的步数开始跳(一定是 2^i),如果跳的到的位置一样,就不跳,如果不一样才跳,每次跳的路程是前一次的一半过程大概就像上图所示,但是执行完了这一段到的点不是最近公共祖先,但是,它们再往上跳一格,就到了。
代码示例
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
const int maxn = 500000 + 2;
int n, m, root;
int k = 0;
int head[maxn], depth[maxn], pmaxn;
//head数组记录点的出边的起始下标,
//depth存的是深度(deep),
//pi存的[i]向上走2的j次方那么长的路径
struct node
{
int v, next;
} e[maxn * 2]; //邻接表(链式前向星)存树
void add(int u, int v)
{
e[k].v = v;
e[k].next = head[u];
head[u] = k++;
} //加边函数
void dfs(int u, int fa)
{
depth[u] = depth[fa] + 1;
pu = fa; //u向上跳2^0(1)个点是其父节点
for (int i = 1; (1 << i) <= depth[u]; i++)
pu = pp[u][i - 1]; //画图思考,不会重复,很高效,因为从上到下添加点及其父节点
for (int i = head[u]; i != -1; i = e[i].next)
{
int v = e[i].v;
if (v != fa)
dfs(v, u);
}
} //首先进行的预处理,将所有点的deep和p的初始值dfs出来
int lca(int a, int b)
{
//非常标准的lca查找
//将深度置为相同
if (depth[a] > depth[b])
swap(a, b); //保证a是在b结点上方,即a的深度小于b的深度
for (int i = 20; i >= 0; i--)
if (depth[a] <= depth[b] - (1 << i))
b = pb;
//如果b的祖先为a,那就可以直接返回答案了
if (a == b)
return a;
for (int i = 20; i >= 0; i--)
{
if (pa == pb)
continue;
else
a = pa, b = pb; //A和B一起上移
}
return pa; //找出最后a值的父节点
}
int main()
{
memset(head, -1, sizeof(head));
int a, b;
scanf("%d%d%d", &n, &m, &root);
for (int i = 1; i < n; i++)
{
scanf("%d%d", &a, &b);
add(a, b);
add(b, a); //无向图,要加两次
}
dfs(root, 0);
for (int i = 1; i <= m; i++)
{
scanf("%d%d", &a, &b);
printf("%d ", lca(a, b));
}
return 0;
}